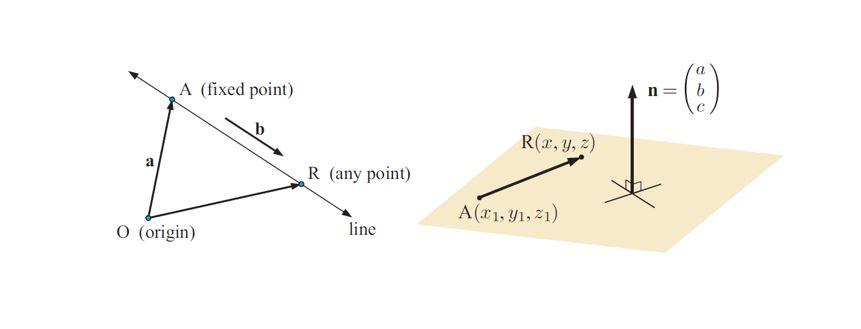
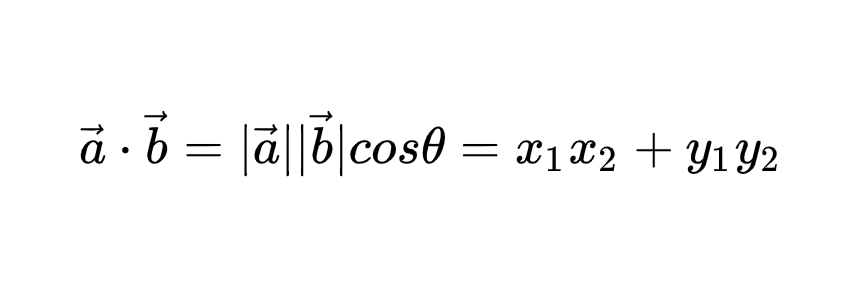在《直线与平面的向量表示》一文中介绍了三维空间的直线、平面的表示，本文就来介绍一下如何计算线线角、线面角、面面角(分别是直线与直线所成的夹角、直线与平面所成的夹角以及平面与平面所成的夹角)。
计算上述三种夹角都借助向量的点乘 以及直线的方向向量与平面的法向量, 如果不熟悉可以参看下文
一、线线角
计算两条直线所成夹角，只需要知道两条直线的方向向量，
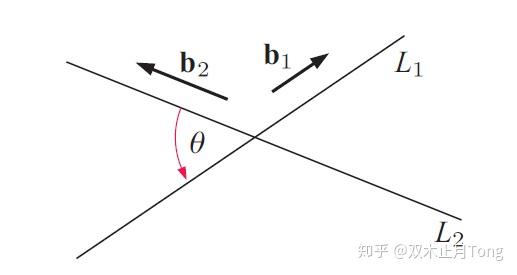
根据向量点乘可知：
而两条直线所成的夹角范围是 ,所以
,
因此， (加绝对值了！)。
再根据反三角函数就能得到两条直线的夹角:
。
二、线面角
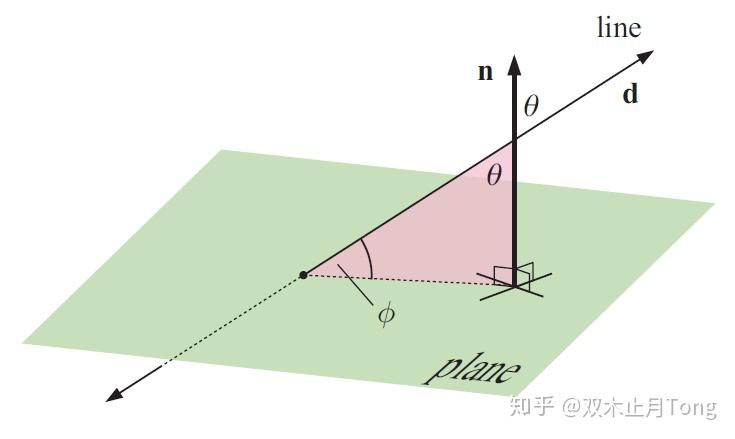
如上图，直线与平面的夹角为 ，但是这个角不好算，但直线与平面法线所成的夹角是好算的，根据上述线线角的求法就知道了。
又因为
所以
因此， ,
。
三、面面角
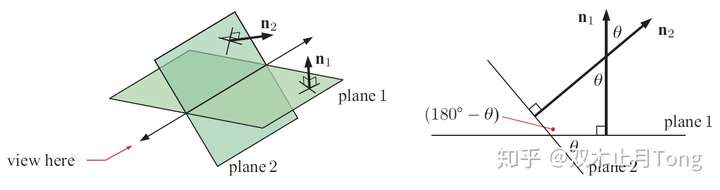
与线线角、线面角类似，我们定义两平面的夹角为所成角中较小的角。通过上图，可以很清楚的看到两个平面法向量所成的夹角就等于两平面所成的夹角。
于是， ,
。
注：国内高中教材二面角取值范围为 ,但是IB教材是
这里可以看一道2014年IB五月真考Paper1第12题：
（a）根据直线 过AB两点可知
。
（b） 。因为
所以
不平行。又因为不存在
使得
方程组成立，所以
不存在交点，故异面。
（c）平面 的法向量为：
，
的方向向量为
,根据直线与平面夹角计算公式：
,
两边平方化简后可得： ,因此
。
所以， 。
要求直线与平面的交点则联立方程：
,
,
因此交点为：